搜索、归并与排序的并行算法

发表于

(并行与分布式计算三)

并行搜索的基本思想

在升序数组中采用与二分搜索类似的p+1分搜索:

  • 使用递归按比例缩小搜索范围的办法
  • 二分搜索每层递归中加入一次比较，p+1分搜索每层递归中加入p次比较
  • 上述的每层p次比较可以用p个处理器同时进行

长度为n的升序数组，用p个处理器做p+1分搜索，并行时间为$O(log_{p+1}(n+1))$

例：p+1分并行搜索:
X=(2,4,6,…,30)，X[1]=2, X[15]=30; Y=9

作p+1分并行搜索，p=2:

  • 迭代1：q0=0, q1=5, q2=10, q3=16
  • 迭代2：q0=5, q1=6, q2=7, q3=10
  • 迭代3：q0=7, q1=8, q2=9, q3=10

快速并行搜索算法

Algorithm 4.1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
(Parallel Search for Processor P_j)
Input: (1)An array X = (x_1, x_2, ..., x_n) such that x_1 < x_2 <       ... < x_n;
       (2)an element y;
       (3)the number p of processors, where p <= n;
       (4)the processor number j, where 1 <= j <= p.
Output: An index i such that x_i <= y < x_i+1.
begin
1. if (j = 1) then do
    1.1 Set l := 0; r := n + 1; x_0 := -∞; x_n+1 := +∞
    1.2 Set c_0 := 0; c_p+1 := 1
2. while (r - 1 > p) do
    2.1 if (j = 1) then {set q_0 := l; q_p+1 := r}
    2.2 Set q_j := l + j*floor((r-1)/(p+1))
    2.3 if (y = x_q_j) then {return (q_j); exit}
        else {set c_j := 0 if y > x_q_j and c_j := 1 if y < x_q_j}
    2.4 if (c_j < c_j+1) then {set l := q_j; r := q_j+1}
    2.5 if (j = 1 and c_0 < c_1) then {set l := q_0; r := q_1}
3. if (j <= r - l) then do
    3.1 Case statement:
        y = x_l+j : {return (l + j); exit}
        y > x_l+j : set c_j := 0
        y < x_l+j : set c_j := 1
    3.2 if (c_j-1 < c_j) then return (l + j - 1)
end

  1. 初始化
  2. 外层搜索递归调用内层搜索
  3. 最内层搜索

$T = O(log_{p+1}(n+1)) = O(\frac{log(n+1)}{log(p+1)}) = O(1)$

并行归并的基本思想

并行地归并两个升序数组，可以等价为计算：
1.归并序=自序+交叉序
2.自序=数组元素在自己所在数组中的序
3.交叉序=数组元素在另一个数组中的序

  • 自序是已知的，交叉序可以用快速并行搜索算法来计算

交叉序的并行搜索的两层并行性:

  • 单个元素的快速搜索内部并行
  • 不同元素的搜索之间并行

例：并行归并中的交叉序计算

A=(-5,0,3,4,17,18,24,28)
B=(1,2,15,21)
分两个迭代并行搜索

迭代1：定位b2和b4。b_2=2在a_2=0和a_3=3之间，b_4=21在a_6=18和a_7=24之间(rank(b_2:A)=2, rank(b_4:A)=6)
迭代2：在b_2前的A元素中搜索b_1的位置，在b_2后、b_4前的A元素中搜索b_3的位置(rank(b_1:A)=2, rank(b_3:A)=4)

并行归并的加速技巧

思路：双层对数树，利用处理器的冗余性加速

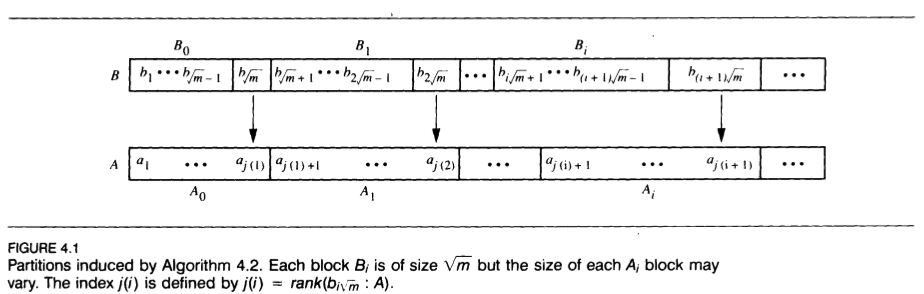
  • 设要计算长度为m的数组B的元素在长度为n的数组A中的交叉序，则由加速层叠法：

  • 最上层分叉成长度为$\sqrt{m}$的段计算，每往下一层长度再开根号

  • 最上层每段使用\sqrt{n}个处理器来并行搜索(共\sqrt{mn}个处理器)，从而分划数组A供下层递归使用
  • 全局来说，每一层都使用不超过(m+n)/2个处理器，并且每层搜索时间T=O(1)

merging1.png

  • 迭代1分割的A段长短不一不会影响加速算法中的处理器上界

最上层$\sqrt(m)$段，对段的右端点在长度为n的A中搜索，求交叉序(能用$\sqrt(n)$个处理器)

  1. $T = O(log{\sqrt(n)+1}(n+1)) = O(log{\sqrt(n)}n) = O(2) = O(1)$
  2. 处理器个数$\sqrt m\sqrt n \leqslant \frac{m+n}{2}$

第二层设B中第i段的右端点切到的A的段的长度为n，B分成$m^{\frac{1}{4}}n^{\frac{1}{4}}$段。第i段用$\sqrt{n_{|\frac{i-1}{\sqrt{m}}|+1}}$个处理器

  • 总处理器数 = $\sum{i=1}^{m^{\frac{3}{4}}}\sqrt{n{|\frac{i-1}{\sqrt{m}}|+1}} = \sum_{j=1}^{\sqrt{m}}m^{\frac{1}{4}}\sqrt{nj} \leqslant \sum{j=1}^{\sqrt{m}}\frac{\sqrt{m}+nj}{2} = (\sum{j=1}^{\sqrt{m}}\sqrt{m} + \sum_{j=1}^{\sqrt{m}}n_j)/2 = (m+n)/2$

第三层处理器个数 = $\sum_{j=1}^{m^{\frac{3}{4}}}m^{\frac{1}{8}}\sqrt{n_j^{(1)}} \leqslant = (\sum m^{\frac{1}{4}} + n_j^{(1)})/2 = (m+n)/2$

  • 其中$n^(1)$是第二层分出的A的$m^{\frac{3}{4}}$段的长度

并行求交叉序

Algorithm 4.2

1
2
3
4
5
6
7
8
9
(Ranking a Sorted Sequence in Another Sorted Sequence)
Input: Two arrays A = (a_1, ..., a_n) and B = (b_1, ..., b_m) in increasing order. Assume that sqrt(m) is an integer; otherwise, replace sqrt(m) whenever it occur by floor(sqrt(m)).
Output: The array rank(B : A)
begin
1. If m < 4, then rank the elements of B by applying the parallel-search algorithm(Algorithm 4.1) with p = n, and exit.
2. Concurrently rank the elements b_sqrt(m), b_2sqrt(m), ..., b_i*sqrt(m), ..., b_m in A by using the parallel-search algorithm(Algorithm 4.1) with p = sqrt(n). Let rank(b_i*sqrt(m) : A) = j(i), for 1 <= i <= sqrt(m). set j(0) = 0.
3. For 0 <= i <= sqrt(m)-1, let B_i = (b_i*sqrt(m)+1, ..., b_(i+1)*sqrt(m)-1) and let A_i = (a_j(i)+1, ..., a_j(i+1)); if j(i) = j(i+1), then set rank(B_i : A_i) = (0, ..., 0), else recursively compute rank(B_i: A_i).
4. Let 1 <= k <= m be an arbitrary index that is not a multiple of sqrt(m), and let i = floor(k/sqrt(m)). Then rank(b_k : A) = j(i) + rank(b_k : A_i)
end

  • |A| = n, |B| = m, T = O(log logm), W = O((n + m)log logm)

最优的并行求交叉序

前一个算法的问题：

  • 运算量O((m+n)log log m)不是最优
  • 最优运算量应该是O(m+n)

解决办法：

  • 在两边数组均匀步长地抽取元素，缩短求交叉序的并行算法的输入数组
  • 用前述并行算法求交叉序
  • 利用抽取的点把两边的数组分段，这边的段一一对应地归并

两个长度都为n的升序数组，可以在O(log log n)的并行时间内用O(n)的运算量归并

merge_fast.png

merge_fast2.png

  • 在A和B中都先均匀采样，对两边采样点计算缩短的数组的交叉序，然后再利用该交叉序来进一步计算原来的数组的交叉序

merging2.png

merging3.png

T = O(log logn), W = O(n)

一个快速并行归并排序算法

  • 从长度为较小常数的数组开始，逐层两两归并，共log n层
  • 每层用O(log log n)的并行时间和O(n)的运算量来归并
  • 总共O(log n log log n)的并行时间和O(n log n)的运算量

Algorithm 4.3

1
2
3
4
5
6
7
8
9
10
(Simple Merge Sort)
Input: An array X of order n, where n = 2^l for sime integer l.
Output: A balanced binary tree with n leaves such that, for each 0 <= h <= logn, L(h, j) contains the sorted subsequence consisting of the elements stored in the subtree rooted at node(h, j), for 1 <= j <= n/2^h. That is node(h, j) contains the sorted list of the elements X(2^h*(j-1) + 1), X(2^h*(j-1) + 2), ..., X(2^h*j)
begin
1. for 1 <= j <= n pardo
    Set L(0, j) := X(j)
2. for h = 1 to logn do
    for 1 <= j <= n/2^h pardo
        Merge L(h-1, 2j-1) and L(h-1, 2j) into the sorted list L(h, j)
end