列表和树

发表于

(并行与分布式计算二)

列表排序

The list-ranking problem is to determine the distance of each node i from the end of the list

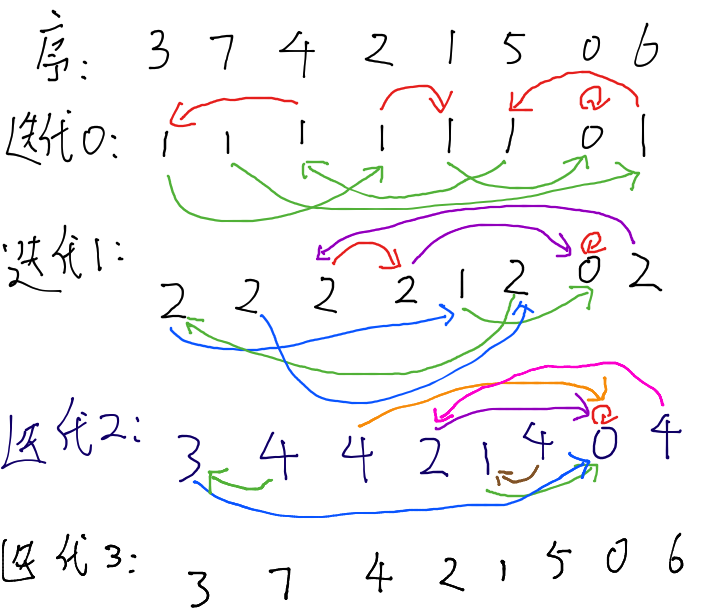
指针跳转法(pointer jumping technique)

思想：

  • 链表中的指针跳转可以由一次跳转一步改为一次跳转多步
  • 如果能在O（1）时间内一次跳转k步，那么一次跳转2k步只需要双倍时间
  • 如果为每个节点，把一次跳转2k步的跳转结果记录下来，那么以后一次跳转2k步也只需要O（1）时间
  • 反复利用跳转步数翻倍和跳转结果记录的技巧，可以在O（log N）的时间内把跳转步数扩大为N

T = O(logn); W = O(nlogn)
并不比串行算法(linear, O(n))更优

list_rank_pointer_jump.png

Algorithm 3.1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# List Ranking Using Pointer Jumping
Input: A linked list of n nodes such that (1)the successor of each node i is given by S(i), and (2)the S value of the last node on the list is euqal to 0.
Output: For each 1 <= i <= n, the distance R(i) of node i from the end of the list.
begin
1. for 1 <= i <= n pardo
    if (S(i) != 0) then set R(i):= 1
                   else set R(i):= 0
2. for 1 <= i <= n pardo
    set Q(i) := S(i)
    while (Q(i) ！= 0 and Q(Q(i)) != 0) do
        set R(i) := R(i) + R(Q(i))
        set Q(i) := Q(Q(i))
end

优化思路:

  • 用快速并行算法把链表长度缩短为n/log n
  • 要求：缩短和恢复都可以用很小的T，并且W=O(n)
  • 方法：通过删除链表中的独立顶点集来缩短链表
  • 在缩短的链表上用指针跳转法来求序，只需W=O(n)
  • 最后用快速并行算法来恢复链表的长度

也即：

  1. 把列表分成约n/logn块{ $B_{i}$ }, 每块包含O(logn)个节点
  2. 在每块内对每个节点用最优串行算法求序(preliminary rank)
  3. 用O(logn)的平行算法把所有排好序的块组合

List-Ranking Strategy

  1. Shrink the linked list L until only O(n/logn) nodes remain.
  2. Apply the pointer jumping technique(Algorithm 3.1) on the short list of the remaining nodes.
  3. Restore the original list and rank all the nodes removed in step 1.

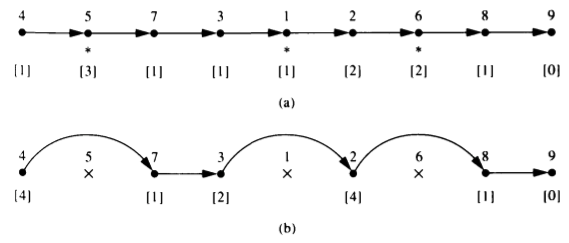
independent sets

  • A set I of nodes is independent if, whenever i belongs to I, S(i) not belongs to I.

缩减的列表结点必须构成一个独立集，即不相邻

shrink_list1.png

shrink_list2.png

Algorithm 3.2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# removing nodes of an independent set
Input: (1)Arrays S and P of length n representing, respectively, the successor and predecessor relations of linked list; (2)an independent set I of nodes such that P(i), S(i) != 0; (3)a value R(i) for each node i.
Output: The list obtained after removal of all the nodes in I with the updated R values.
begin
1. Assign consecutive serial numbers N(i) to the elements of I, where 1 <= N(i) <= |I| = n'.
2. for for all i belongs to I pardo 
    set U(N(i)) := (i, S(i), R(i))
    set R(P(i)) := R(P(i) + R(i))
    set S(P(i)) := S(i)
    set P(S(i)) := P(i)
end

删除独立顶点集并合并其权重到剩余顶点的并行复杂度: T=O(1) W=O(n)

Determination of an Independent Set

独立集合充分大：存在常数c，c属于(0, 1)，使集合包含顶点数不少于c×n

  • 保证快速地迭代缩短链表
  • 把长度为n的链表缩短为n/logn只需不超过log_1-c(logn)的T

最理想但没有快速算法：用序的奇偶性确定独立顶点集合，c=1/2

(存在快速算法)对链表使用三色着色算法，把局部最小色数(或最大)的节点作为独立集元素

coloring.png

  • 从一个局部极小到下一个局部极小着色点，中间经过的点数最多为3，因此C=1/4
  • 3-color 算法收敛很快，每次调用算法，
    着色的色数都变小为原色数的对数比例，这里的对数以2为基底
  • 要把色数变小为3，T几乎是O(1)

Algorithm 3.3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# simple optimal list ranking
Input: A linked list with n nodes suc that the successor of each node i is given by S(i).
Output: For each node i, the distance of i from the end of the list.
begin
1. set n_0 := n, k := 0
2. while n_k > n/logn do
    2.1 set k := k + 1
    2.2 color the list with three colors and identify the set I of local minima.
    2.3 remove the nodes in I, and store the appropriate information regarding the removed nodes(Algorithm 3.2).
    2.4 let n_k be the size of the remaining list. compact the list into consecutive memory locations.
3. apply the pointer jumping technique (Algorithm 3.1) to the resulting list.
4. restore the original list and rank all the removed nodes by reversing the process performed in step2.
end

缩短链表和恢复链表：T = O(log logn), W = O(n)

  • 把长度为n的链表缩短为n/logn，只需不超过log_1-c(logn)的T
  • 第一次迭代W = O(n), 第二次迭代W = O((1 - c)*c), …
  • W = O(n + (1 - c)n + (1 - c)^2 *n + …) = O(n/c) = O(n)
  • 恢复和缩短是对称的，T和W都相同

指针跳转是在长度为n/logn的已缩短链表上zuo做的，T = O(logn), W = O(n)

算法的并行复杂度: T = O(loglogn); W = (n)

  • *一个优化的时间复杂度为O(logn)的列表求序算法……

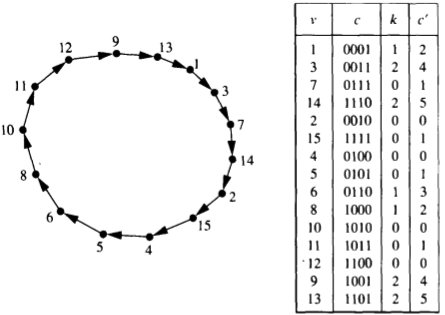
欧拉回路(the Euler-Tour Technique)

树的欧拉回路是指：
将一棵树的每一条边换成两条指向相反的有向边，成为一个欧拉图，就存在欧拉回路；
可以定义一个论域为所有有向边的函数s(successor function)，描述这棵树的欧拉回路

Lemma 3.6: Given a tree T = (V, E) and an ordering of the set of vertices adjacent to each vertex v belongs to V, the function s defined previously specifies an Euler circuit in the directed graph T’ = (V, E’), where E’ is obtained by replacement of each e belongs to E by two arcs of opposite directions.

  • we call the Euler circuit of T’ the Euler tour of T

  • 每棵树都有欧拉回路

  • 如果欧拉回路从树的根节点出发，则它实际上是树的节点深度优先遍历路径

给出一个由邻接表及附加的指针信息描述的树，求得一条欧拉回路的T = O(1), W = O(n), |V| = n
(指针信息: data field + pointer * 2(描述下一个邻接点 + 描述该点在邻接表中指向此顶点的item))

  • 树求根(rooting a tree): 树根结点为r，对于每个非根结点v，寻找其父父结点p(v)

  • 一对顶点之间的两条弧，先出后进的顶点是父节点，先进后出的是子节点

弧的顺序的确定：
-把欧拉回路从其中一点处断开（例如去除回路路径列表中的最前与最后的弧的相邻关系）

  • 用链表求序来对这些弧定序

树的一个欧拉回路为L[r] = < u_0, u_1, … , u_d-1 >

设s(< u_d-1, r >) = 0，将欧拉回路从r处截断，得到一条始于r，遍历所有顶点一次，终于r的欧拉路径

Algorithm 3.5

1
2
3
4
5
6
7
8
9
10
11
# rooting a tree
Input: (1)a tree T defined by the adjacency lists of its vertices, (2)an Euler tour defined by the successor function s, and (3)a special vertex r
Output: For each vertex v != r, the parent p(v) of v in the tree rooted at r.
begin
1. Identify the last vertex u appearing on the adjacency list of r. set s(<u, r>) = 0
2. Assign a weight of 1 to each arc <x, y>, and apply parallel prefix on the list of arcs defined by s.
3. For each arc <x, y>, set x = p(y) whenever the prefix sum of <x, y> is smaller than the prefix sum of <y, x>.
end

并行复杂度与链表求序相同：

  • T=O(log n log log n) ？？？
  • W=O(n)
  • 这里n是顶点数（树的边数是顶点数减一）

1、Postorder Numbering 后序遍历的序数

往下走的弧的权重为0，往上走的弧的权重为1，然后用链表中求前缀和的方法来算出后序遍历编号

Algorithm 3.6

1
2
3
4
5
6
7
8
9
10
11
# Postorder Numbering
Input: (1)A rooted binary tree with root r, and (2)the coresponding Euler path defined by the function s
Output: The postorder number post(v) of each vertex v
begin
1. For each vertex v != r, assign the weights w(<v, p(v)>) = 1 and w(<p(v>, v) = 0
2. Perform parallel prefix on the list of arcs defined by s.
3. For each vertex v != r, set post(v) equal to the prefix sum of <v, p(v)>. For v = r, set post(v) = n, where n is the number of vertices in the given tree.
end

2、Computing the Vertex level 结点层数

可用类似Algorithm 3.6的算法，1和3做改动: w() = +1; w() = -1。level(v) = 的前缀和

3、Computing the preorder Number

w(< p(v), v >) = 1; w(< v, p(v) >) = 0;

preorder(v) = < p(v), v >前缀和 + 1; preorder(r) = 1

4、Computing the Number of Descendants

w(< p(v), v >) = 1; w(< v, p(v) >) = 0;

desc(v) = < v, p(v) >前缀和 - < p(v), v >前缀和; desc(r) = n - 1

以上四个并行算法:
T = O(logn); W = O(n)（由平衡树方法求前缀和的平行算法所决定）

  • *Tree Contraction(树收缩) ……
  • *Lowest Common Ancestors ……