并行计算基础知识及基本并行算法

(并行与分布式计算一)

基础知识

设计分布式并行算法基本流程

1.1发现计算问题的内在并行性

1.2设计与硬件无关的并行算法

• 让算法设计者专注于挖掘问题相关的内在并行性而不是被繁琐的硬件特性所干扰

• 便于不同硬件环境下的开发者移植算法

• 便于算法到硬件的映射的自动匹配和优化

• 为并行和分布式计算的系统库(中间件)研发提供一套高层语义抽象

PRAM(Parallel Random Access Machine, 随机存取并行机器): 一个简单的并行算法模型

• Parallel: 可以自由分布任意个处理器并行地读、写和计算

• Random Access: 处理器可以按下面其中一条规则自由地访问“共享内存”

1. 规则一: Exclusive Read Exclusive Write(EREW)(不允许同时读和同时写)

2. 规则二: Concurrent Read Exclusive Write(CREW)(允许同时读但不允许同时写)

3. 规则三: Concurrent Read Concurrent Write(CRCW)(允许同时读和同时写)

• 算法复杂度框架: work(计算量(operation)), time(计算时间)

2.1发现硬件的网络拓扑和处理能力

网络拓扑:

• 静态: 环、星、树、超立方、图
• 动态: 互联网或移动网络中的分布式计算

处理能力:

• 指标: 处理速度和处理规模
• 结构: 同构、异构
• 方式: 内存计算还是内外存混合计算，计算密集型还是数据密集型

发现网络拓扑的算法:

• 目的一: 建立数据通信的路由
• 目的二: 死锁检测和解除
• 目的三: 优化数据传播和交换

发现处理能力的方法:

• 测试程序
• 人工检测

2.2设计与计算问题无关的分布式计算协议

(所需计算协议包括以下但不止)

• 广播、多播和数据收集

• 同步和异步控制

• 终止检测和全局谓词(条件)检测

• 快照保存与检查点恢复

3.把并行算法映射到硬件上，匹配、优化

匹配:

• 与硬件相关的具体并行算法
• 数据分划和任务指派方案(静态或动态)
• 并行和分布式计算的程序

优化:

• 面向硬件体系结构的算法复杂度分析
• 针对硬件特性的算法改进和程序调优

并行计算的基本方法

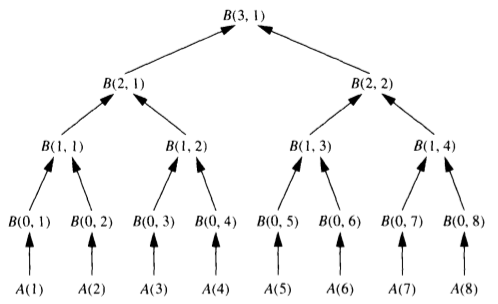
平衡树方法(Balanced Trees)

• 例: 设是满足结合律的二元运算符，考虑计算
  $$ S_i = x_1 x_2 … x_i, 1 \leq i \leq n $$

Algorithm 2.1

# Prefix Sums

Input: An array of n = 2^k elements (x_1, x_2, ..., x_n), where k is a nonnegative integer.

Output: The prefix sums s_i, for 1 <= i <= n.

begin
1. if n = 1 then {set s_1 := x_1; exit}
2. for 1 <= i <= n/2 pardo
    set y_i := x_2i-1 * x_2i
3. Recursively, compute the prefix sums of {y_1, y_2, ..., y_n}, and store them in z_1, z_2, ..., z_n/2
4. for 1 <= i <= n pardo
    {i even     :  set s_i := z_i/2
     i = 1      :  set s_1 := x_1
     i odd > 1  :  set s_i := z_(i-1)/2 * x_i}
end

• 复杂度分析
  $$ T(n) = T(\frac{n}{2}) + a $$
  $$ W(n) = W(\frac{n}{2}) + bn $$
  求解递归方程
  $$ T(n) = O(logn) $$
  $$ W(n) = O(n) $$

Algorithm 2.2

# Nonrecursive Prefix Sums

Input: An array A of size n = 2^k, where k is a nonnegative integer.

Output: An array C such that C(0, j) is the jth prefix sum, for 1 <= j <= n

begin
1. for 1 <= j <= n pardo
    set B(0, j) := A(j)
2. for h = 1 to logn do
    for 1 <= j <= n/2^h pardo
        set B(h, j) := B(h - 1, 2j - 1) * B(h - 1, 2j)
3. for h = logn to 0 do
    for 1 <= j <= n/2^h pardo
        {j even    : set C(h, j) := C(h + 1, j/2)
         j = 1     : set C(h, 1) := B(h, 1)
         j odd > 1 : set C(h, j) := C(h + 1, (j - 1)/2)*B(h, j)}
end

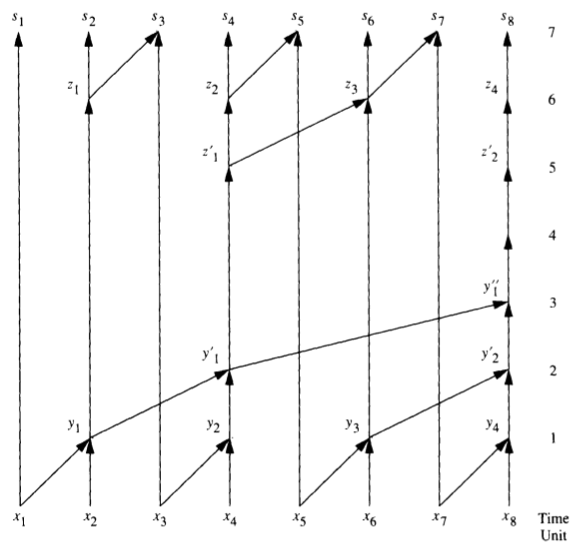
指针跳转法(Pointer Jumping)

• 例一: 存储在数组中的链表求序

• 串行算法: 线性复杂度
• 并行复杂度: T = O(logn), W = O(nlogn)

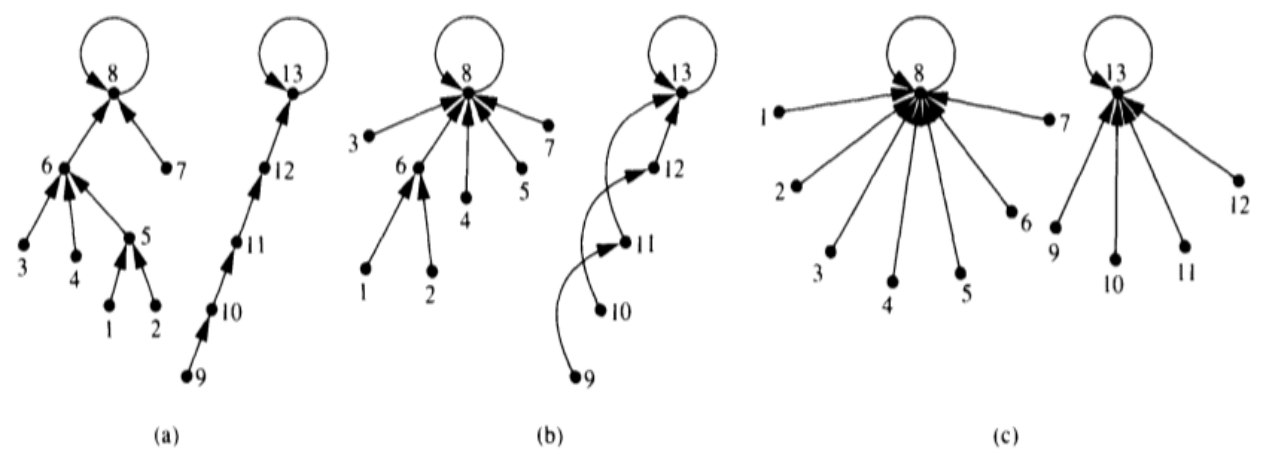
• 例二: 为森林里的每个节点找所在的那棵树的根节点

Algorithm 2.4

# Pointer Jumping

Input: A forest of rooted directed trees, each with a self-loop at its root, such that each arc is specified by (i, P(i)), where 1 <= i <= n.

Output: For each vertex i, the root S(i) of the tree containing i.

begin
1. for 1 <= i <= n pardo
    set S(i) := P(i)
    while (S(i)) != S(S(i)) do
        set S(i) := S(S(i))
end

T = O(logh); W = O(nlogh)

Algorithm 2.5

# Parallel Prefix on Rooted Directed Trees

Input: A forest of rooted directed trees, each with a self-loop at its root such that (1)each arc is specified by (i, P(i)), (2)each vertex i has a weight W(i), and (3)for each root r, W(r) = 0

Output: For each vertex i, W(i) is set equal to the sum of the weights of vertices on the path from i to the root of its tree.

begin
1. for 1 <= i <= n pardo
    set S(i) := P(i)
    while (S(i)) != S(S(i)) do
        set W(i) := W(i) + W(S(i))
        set S(i) := S(S(i))
end

T = O(logn); W = O(nlogn)

分而治之法(Divide and Conquer)

例: 找二维平面上的点的凸包(planar convex hull)

• 分: 把这些顶点按由左到右平均分成两组
• 治: 在这两组内分别求凸包(求解两个规模相对较小的问题，递归)
• 合: 把两组凸包用快速算法合为一个

Algorithm 2.6

# Simple Upper Hull

Input: A set S of n points in the plane, no two of which have the same x or y coordinates such that x(p_1) < x(p_2) < ... < x(p_n), where n is a power of 2.

Output: The upper hull of S.

begin
1. If n <= 4, then use a brute-force method to determine UH(S), and exit.
2. Let S_1 = (p_1, p_2, ..., P_n/2) and S_2 = (p_n/2+1, ..., p_n). Recursively, compute UH(S_1) and UH(S_2) in parallel.
3. find the upper common tangent between UH(S_1) nad UH(S_2), and deduce the upper hull of S.
end

$$ T(n) \leq T(\frac{n}{2}) + alogn $$
$$ W(n) \leq 2W(\frac{n}{2} + bn) $$
并行复杂度: $ T = O(log^2 n); W = O(nlogn) $

数据划分法(partition strategy)

• 例: 归并排序

• 1.数据均分为若干等分
• 2.在每一等分内用其它方法排序
• 3.平衡树快速并行合并这些等分

Algorithm 2.7

# Partition

Input: Two arrays A = (a_1, a_2, ..., a_n) and B = (b_1, b_2, ..., b_m) in increasing order, where both logm and k(m) = m/logm are integers.

Output: k(m) pairs (A_i, B_i) of subsequences of A and B such that (1)|B_i| = log m, (2)\sum |A_i| = n, and (3)each element of A_i and B_i is larger than each element of A_i-1 or B_i-1, for all 1 <= i <= k(m)-1

begin
1. set j(0) := 0, j(k(m)) := n
2. for 1 <= i <= k(m) - 1 pardo
    2.1. Rank b_ilogm in A using binary search method, and let j(i) = rank(b_ilogm : A)
3. for 0 <= i <= k(m) - 1 pardo
    3.1. set B_i := (b_ilogm+1, ..., b_(i+1)logm)
    3.2. set A_i := (a_j(i) + 1, ..., a_j(i+1))
        (A_i is empty if j(i) = j(i+1))
end

• 合并后的序 = 自序 + 交叉序
• 自序(a_i) = {a_0, a_1, …, a_n-1}中有多少a_j 排在a_i前面(在这里即i)
• 交叉序(a_i) = {b_0, b_1, …, b_n-1}中有多少b_j排在a_i前面

并行复杂度: T = O(logn); W = O(n)

流水线方法(Pipelining)

• 例: 2-3树的数据插入

• 批量插入多个点及其并行复杂度
  T = O(logn); W = O(klogn)

• breaking up a task into a sequence of subtask t_1, t_2, …, t_m
  ……

加速层叠法(Accelerated Cascading)

• 例: 数组找最大值

常数的并行时间复杂度

Algorithm 2.8

# Basic Maximum

Input: An array A of p distinct elements.

Output: A Boolean array M such that M(i) = 1 if and only if A(i) is the maximum element of A.

begin
1. for 1 <= i, j <= p pardo if (A(i) >= A(j)) then set B(i, j) := 1
                                              else set B(i, j) := 0
2. for 1 <= i <= p pardo
    set M(i) := B(i, 1) & B(i, 2) & ... B(i, p)
end

$ T = O(1); W = O(p^2) $

双层log深度树(doubly logarithmic-depth tree): 最底层节点数 为 n，根节点的孩子节点数 为 $n^{\frac{1}{2}}$，下一层每个节点的孩子节点数 $n^{\frac{1}{2^2}}$，…

• 假设$n = 2^{2^k}$, 树根有$2^{2^{k-1}}$个孩子, 第一层有$2^{2^{k-2}}$个孩子, …, 第i层有$2^{2^{k-i-1}}$个孩子, …

• 倒数第二层每个节点有常数个子节点

• 向上合并用常数复杂度求最大值方法
• 整体并行复杂度: $$ T(n) = O(log log n) $$ $$ W(n) = O(n log log n) $$

accelerated cascading:

1. start with the optimal algorithm until the size of the problem is reduced to a centain threshold value. 双层log深度树加速
2. Then, shift to the fast but nonoptimal algorithm. 常数时间算法层叠

对称破坏法(Symmetry Breaking)

• 例: 环的三色着色问题

• 要求: 相邻的点不能是相同的颜色
• 串行算法: 在环上随机选一点把环打开得到一个队列；从队首开始除队尾外以0，1相间着色，队尾着色为2(确保队尾和队首、对中倒数第二节点的颜色都不同)
• 并行算法大致思想: 从以节点编号为颜色的着色方案开始，通过迭代算法，逐步减少着色数量

Algorithm 2.9

# Basic Coloring

Input: A directed cycle whose arcs are specified by an array S of size n and a coloring c of the vertices.

Output: Another coloring c' of the verteces of the cycle.

begin
for 1 <= i <= n pardo
    1. set k to the least significant bit position in which c(i) and c(S(i)) disagree.
    2. set c'(i) := 2k + c(i)_k
end

T = O(1); W = O(n)

definition: $log^{(1)}x = logx$, and $log^{(i)}x = log(log^{(i-1)}x)$

• Fast Coloring
  反复运用这个算法使得从颜色序号{0, 1, 2}中重新选择颜色给每个顶点着色且相邻顶点色不同, 整体并行复杂度为: $$ T = O(logn); W = O(nlogn) $$

Algorithm 2.10

# 3-coloring of a Cycle

Input: A directed cycle of length n whose arcs are specified by an array S.

Output: A 3-coloring of the vertices of the cycle.

begin
1. for 1 <= i <= n pardo
    set C(i) := i
2. Apply Algorithm 2.9 once.
3. Sort the vertices by their colors.
4. for i = 3 to 2 \ceiling(logn) do
    for all vertices v of color i pardo
    color v with the smallest color from {0, 1, 2} that is diffrrent from the colors of its two neighbors.
end

T = O(logn); W = O(n)

• 三色环着色过程

1. 迭代调用算法2.9，把颜色降至c种以下(c是较小常数，如10等)
2. 遍历从3到c-1种颜色:
   for(color = 3; color < c; ++color) {
   环中结点号i
   if i的颜色为color pardo

   根据左右邻居占用3颜色0,1,2中的哪几种，决定结点i可以取得颜色({0,1,2}中的某一个)
   

   }

在1.中，设迭代t的颜色数为$nt$，则$n{t+1} \leqslant 2(\ulcorner log_2n_t \urcorner - 1) + 1$